Empezamos con el circuito lógico puesto en la esquina inferior izquierda, obteniendo del mismo la expresión de su salida lógica Out puesta en la esquina superior izquierda:
Out = AB + AB + AB
Esta expresión está justo en la forma que requerimos (suma de productos) para construír el mapa de Karnaugh usando minterms. El término AB nos produce un "1" cuando A=0 y B=1, y esta es nuestra primera entrada en el mapa de Karnaugh. El término AB nos produce un "1" cuando A=1 y B=0, y esta es nuestra segunda entrada en el mapa de Karnaugh. Y por último, el término AB nos produce un "1" cuando A=1 y B=1, y esta es nuestra tercera entrada en el mapa de Karnaugh.
El siguiente paso consiste en llevar a cabo los agrupamientos que nos pueden dar una simplificación del circuito. Estos son mostrados en el mapa de Karnaugh puesto en la esquina superior derecha. El primer agrupamiento como "minterm" más sencillo es la variable A (agrupando los valores de A=1) y el segundo agrupamiento como "minterm" más sencillo es la variable B (agrupando los valores de B=1). Los "minterms" simplificados en el mapa de Karnaugh nos dicen que podemos reemplazar la expresión original por la siguiente expresión (en suma-de-produtos) más simplificada:
Out = A + B
El circuito lógico simplificado se muestra en la esquina inferior derecha del diagrama, el cual requiere un solo componente lógico, un OR, a diferencia del circuito original que requería de cuatro componentes, tres AND y un OR.
Considérese ahora un circuito lógico cuya salida Out está dada por la siguiente expresión:
Out = A·B·C + AB·C + ABC + AB + ABC
Este circuito lógico con tres variables de entrada tiene una salida dada como suma de productos, lo cual nos permite localizar los "1" de los minterms que van dentro del mapa de Karnaugh y lo cual nos permite llevar a cabo la simplificación "enrollando" el mapa alrededor de un cilindro como se muestra:
No resulta difícil ver que la versión simplificada es simplemente:
Out = C
A continuación tenemos otro mapa de Karnaugh, ahora para un circuito con cuatro variables de entrada A, B, C y D, tanto antes como después de haber encontrado un conjunto de posibles simplificaciones:
Existen muchos casos en los cuales no todas las combinaciones lógicas de "ceros" y "unos" a la entrada de un circuito son necesarias; un ejemplo de ello es el de un decodificador que toma un número binario de cuatro bits a su entrada y lo convierte en una combinación de siete salidas para encender selectivamente los segmentos de un indicador luminoso numérico hecho a base de diodos emisores de luz LED; en este caso no se utilizará ninguna de las combinaciones entre "1010" y "1111" puesto que no representan dígito alguno en el sistema numérico decimal. Cuando tenemos algunas condiciones dentro de un circuito lógico en las cuales la salida puede ser ya sea un "0" ó un "1" sin consecuencia alguna para el diseño final (conocidas en la literatura de habla inglesa como condiciones don't care), podemos representar dichas condiciones simplemente con una "X" que se sobreentiende que puede tener un valor de "0" ó de "1". A continuación tenemos otro mapa de Karnaugh para un circuito con cuatro variables de entrada A, B, C, D, y cuatro condiciones "X", tanto antes como después de haber encontrado para dicho circuito un conjunto de posibles simplificaciones:
Por lo general, para un circuito lógico con más de cuatro variables de entrada el uso del mapa de Karnaugh va perdiendo su ventaja visual como instrumento de simplificación. Para un circuito lógico con más de cinco o seis variables de entrada, se recomienda el uso de otro método o inclusive de alguno de varios programas computacionales especializados para lograr minimizar un circuito lógico a su expresión más sencilla, muchos de los cuales están basados en otro método de simplificación de circuitos lógicos que va de la mano con el mapa de Karnaugh, el método de Quine-McCluskey, del cual se dará a continuación una introducción.
El estudio del método de Quine-McCluskey nos lleva a definir de manera más formal cierta terminología que hemos pasado por alto, empezando con la definición de los implicantes primarios (prime implicants). En primer lugar, para una salida Y, un implicante se define como un producto normal de dos o más variables (normal en el sentido de que cada variable en el producto aparece una sola vez, con lo cual se descalifica a expresiones como AAB o ABBC) que implica a Y (esto es, produce un "1" en la columna correspondiente a la salida del circuito en su Tabla de Verdad), como en la expresión:
Y = AB + ABC + BC
en donde los implicantes son AB, ABC y BC porque cualquiera de ellos implica a Y. Definido esto, definimos a continuación a un implicante primario como un implicante de Y tal que si cualquiera de sus variables es removida, el término que nos queda ya no implica a Y. Esto quiere decir que en la expresión anterior AB y BC son implicantes primarios (no es posible remover ninguna de las variables en ellos sin que pierdan su relevancia), mientras que ABC no es un implicante primario ya que si se le remueve la variable A esto nos deja con el término BC que sigue implicando a Y porque dicho término está contenido en la expresión original de Y. El hecho de que un implicante no sea un implicante primario tiene que ver directamente con una simplificación Booleana como la siguiente:
A∙B·C∙D + ABC = A∙B·C(D + 1) = A∙B·C
en la cual el implicante primario ABC se "come" al implicante A∙B·C∙D que contiene la variable D que podemos considerar superflua. Cabe notar que un implicante primario no puede ser reducido más, ya que no contiene ninguna variable que pueda ser "comida" al combinarlo con cualquiera de los otros términos en una expresión Booleana; precisamente por ello es un implicante primario. Es de notar que el método de simplificación de Quine-McCluskey es conocido también como el método de implicantes primarios, siendo funcionalmente idéntico al mapa de Karnaugh pero con una forma tabular que hace más accesible su implementación en programas de computadora (el mapa de Karnaugh por ser un método visual no se presta a la elaboración de un programa de computadora que busque el diseño óptimo sin intervención humana), y el cual es superior al mapa de Karnaugh en el sentido de que siempre garantiza la obtención del diseño más económico posible.
Al cubrir el tema del método de Quine-McCluskey, es rutinario en los libros tecnológicos utilizar una notación en la cual a los minterms se les designa de acuerdo con el valor numérico binario que poseen en su notación de "unos" y "ceros". Esta notación proporciona una manera compacta de listar los minterms de una expresión Booleana, lo cual nos puede resultar conveniente en expresiones con más de cuatro variables. Bajo la notación compacta, en una función Booleana de tres variables el minterm ABC proveniente de la combinación binaria "111" es representado precisamente con dicha combinación binaria, simplificada a su equivalente decimal que es 7, mientras que el minterm A·B·C proveniente de la combinación "000" es representado por el decimal 0. Del mismo modo, un minterm como ABC es representado por "011" o bien por el decimal 3. Esto permite representar una expresión Booleana como:
f(A,B,C,D) = ABC + AB·C + A·BC
como la suma de los minterms cuyos equivalentes decimales son 011 (3), 100 (4) y 001 (1), o más elegantemente usando la letra griega sigma mayúscula (Σ) que indica una suma de términos:
f(A,B,C,D) = Σm(001,011,100)
f(A,B,C,D)= Σm(1,3,4)
f(A,B,C,D)= Σm(1,3,4)
en donde "Σm" se lee como "la suma de minterms"
Del mismo modo, para la siguiente función de tres variables:
Z = f(A,B,C,D) = A·B·C + A·BC + AB·C + ABC
Z = Σm(000,001,100,101)
Z = Σm(0,1,4,5)
Z = Σm(000,001,100,101)
Z = Σm(0,1,4,5)
así como para la siguiente función de cuatro variables:
f(A,B,C,D) = A·B·C·D + A·B·CD + A·BCD + A·BCD + ABCD + ABCD + AB·C·D
+ ABCD + ABC·D + ABCD + ABCD
+ ABCD + ABC·D + ABCD + ABCD
f(A,B,C,D) = Σm(0000,0001,0010,0011,0101,0111,1000,1010,1100,1101,1111)
f(A, B, C, D) = Σm(0,1,2,3,5,7,8,10,12,13,15)
f(A, B, C, D) = Σm(0,1,2,3,5,7,8,10,12,13,15)
Si algún término contiene menos variables que el número total de variables especificado por la Tabla de Verdad, cada variable "ausente" en el término es simbolizada en el sitio que le corresponde con un guión (-). De este modo, para una función Booleana de tres variables, AC es representado como "1-0" y BC es representado como "-11".
Cabe agregar que bajo la notación compacta también podemos representar los términos redundantes X, aquellos cuyo valor no importa que sea "1" ó "0" en el diseño de un circuito lógico. Por ejemplo, para la siguiente Tabla de Verdad en la cual se muestran dos términos redundantes marcados con una "X", los cuales corresponden a los minterms AB·CD y ABCD que en notación compacta vendrían siendo m9 y m14:
la representación en notación compacta usando minterms será:
f(A,B,C,D) = Σm(4,8,10,11,12,15) + d(9,14)
El método Quine-McCluskey, el cual hace uso repetido del axioma Booleano A+A=1, involucra la siguiente secuencia de pasos, la cual es obvia para quien haya tenido ya alguna práctica en el uso de los mapas de Karnaugh:
Primer paso: Se van agrupando los minterms dependiendo de la cantidad de "unos" que tengan en su representación binaria. Esta cantidad es conocida como el índice de la representación (0000 tiene un índice de 0, 0010 y 1000 tienen ambas un índice de 1, 1010 y 0011 y 1001 tienen las tres un índice de 3, y 1111 tiene un índice de 4). Así, en la siguiente expresión Booleana de cinco variables:
F(p,q,r,s,t) = Σm(0,1,3, 4,6,11,14,15,16,18,24,27,28,31)
el agrupamiento de los términos de acuerdo con sus índices es el que se muestra a continuación:
Podemos reemplazar dos términos adyacentes cualesquiera que contengan un solo guión en una posición que corresponda al bit no apareado. Al ir llevando a cabo este procedimiento, para comodidad nuestra, podemos ir "checando" con una "palomita" o "marcando" con una "equis" de alguna manera los minterms que van siendo utilizados para crear términos comunes para que así no sean incluidos nuevamente por equivocación.
Tercer paso: Repetimos la búsqueda hasta que no sea posible encontrar más términos adyacentes. Dos términos adyacentes que contengan guiones son considerados adyacentes solo sí todas las posiciones con guiones se correspondan en ambos términos y todas excepto una sola posición literal contengan el mismo valor. En la expresión Booleana que estamos utilizando como ejemplo, estos pasos aparecen resumidos en la manera que se muestra a continuación (obsérvese que tenemos aquí dos listas, la primera que aparece en el extremo izquierdo, y la lista puesta en el medio y la cual fue obtenida de la primera):
Cuarto paso: Removemos todos los términos que aparezcan duplicados y listamos los términos que sobrevivieron al proceso, indicando cuáles de los minterms originales están cubiertos por los términos sobrevivientes.
Quinto paso: Seleccionamos el número mínimo de implicantes residuales necesarios para cubrir todos los minterms, lo cual puede ser algo laborioso de encontrar conforme aumenta el número de variables. Los últimos pasos están resumidos en el siguiente arreglo reticular en el cual listamos todos los implicantes primarios (en la columna extrema izquierda) y todos los minterms de la función (en el renglón superior), en donde cada minterm cubierto por algún implicante primario es marcado en la posición apropiada:
Sexto y último paso: Recogemos el conjunto seleccionado de implicantes primarios para generar una expresión Booleana minimizada.
Necesariamente, cualquier minimización obtenida bajo el método de Quine-McCluskey contendrá únicamente implicantes primarios.
Tanto el mapa de Karnaugh como el método de Quine-McCluskey se pueden extender para llevar a cabo la simplificación de circuitos lógicos de varias entradas y varias salidas, o sea de entradas múltiples y salidas múltiples, tales como un diseño de tres entradas A, B y C, y dos salidas H1 y H2, cuya Tabla de Verdad sea la siguiente:
Sin embargo, esta situación no involucra la invención de ningún nuevo tipo de mapa de Karnaugh. En realidad, la situación mostrada en este ejemplo requiere de la construcción de dos mapas de Karnaugh, uno para la salida H1 y el otro para la salida H2. Esto es obvio cuando nos damos cuenta de que la Tabla de Verdad mostrada es un resumen de dos Tablas de Verdad, una para H1 y la otra para H2. Del mismo modo, un circuito lógico con tres entradas y cinco salidas requerirá de la construcción de cinco mapas de Karnaugh, uno para cada una de las cinco salidas. La cantidad de salidas de un circuito lógico es la que determina la cantidad de mapas de Karnaugh que serán requeridos para tratar de minimizar los componentes que serán usados. En el ejemplo mostrado, tenemos dos mapas, el mapa correspondiente a la salida H1:
y el mapa correspondiente a la salida H2:
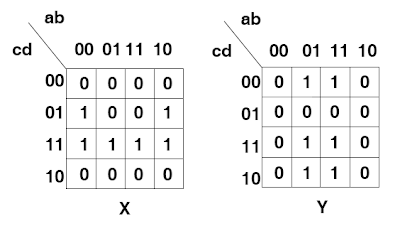
Una vez que tenemos todos los mapas de Karnaugh a la mano, tenemos dos opciones: la primera consiste en tratar de simplificar lo más posible los circuitos correspondientes a cada una de las salidas de manera independiente consultando única y exclusivamente el mapa de Karnaugh que corresponda a cada salida, y es la opción más fácil de todas. La segunda opción consiste en tratar de simplificar las salidas buscando los términos comunes que aparezcan en los mapas y que se puedan agrupar con el fin de evitar repeticiones innecesarias mediante el uso de sub-circuitos que pueden alimentar en forma común a dos o más salidas, lo cual requiere tener todos los mapas lado a lado. A continuación se muestran los mapas de Karnaugh para un circuito lógico con cuatro variables de entrada a, b, c y d, y dos salidas X y Y, en los cuales viéndolos juntos a primera vista se antojan algunas simplificaciones posibles notando las celdas que tienen en común:
La aplicación de los conceptos aquí aprendidos a un circuito multi-salidas para lograr su simplificación óptima se puede convertir en un asunto algo elaborado. Sin embargo, no se entrará más a fondo en un estudio sobre una extensión de la técnica del mapa de Karnaugh (y mucho menos del método de Quine-McCluskey) bajo hoy anticuadas filosofías de economización porque en la práctica con el bajo costo del "hardware" puede salir más caro tener a un ingeniero consumiendo varios días o inclusive varias semanas de su tiempo para lograr la simplificación de un circuito pese a que con el bajo costo actual de la microelectrónica no se logre un ahorro que justifique la inversión del tiempo de ingeniería en estos ejercicios intelectuales. Puesto de otra manera, en la simplificación de circuitos lógicos elaborados hay que tener en cuenta también el factor costo para saber si vale la pena invertir tiempo valioso de ingenieros competentes cuando hay otras técnicas (como el uso de las memorias ROM y PROM que serán tratadas en capítulos posteriores) que han hecho obsoletas las inversiones excesivas en tiempo de diseño. Si en otros tiempos por el alto costo inclusive de un simple inversor lógico NOT construído con un bulbo electrónico como el popular 6SN7 (utilizado ampliamente en la construcción de radios de bulbos y televisores de blanco y negro) era deseable e inclusive necesario economizar todas las funciones lógicas que fuese posible en un diseño, esto es ya una cosa del pasado, y hoy hay que adaptarse a los nuevos tiempos.
Escrito por Archie Tecnology
Si te ha gustado esta entrada y te ha sido de utilidad, por favor, ayuda a otros a encontrarnos con un Me Gusta en Facebook, o , un Twitter. Además para que puedas estar informado puntualmente de nuestras novedades puedes hacerte seguidor de este blog y seguirnos en nuestras redes sociales. Muchas gracias por su confianza, que es por lo que trabajamos y hace superarnos día a día.
ARTÍCULOS RELACIONADOS














Perfecto, gran explicación. Enhorabuena por vuestro blog!!!
ResponderEliminar